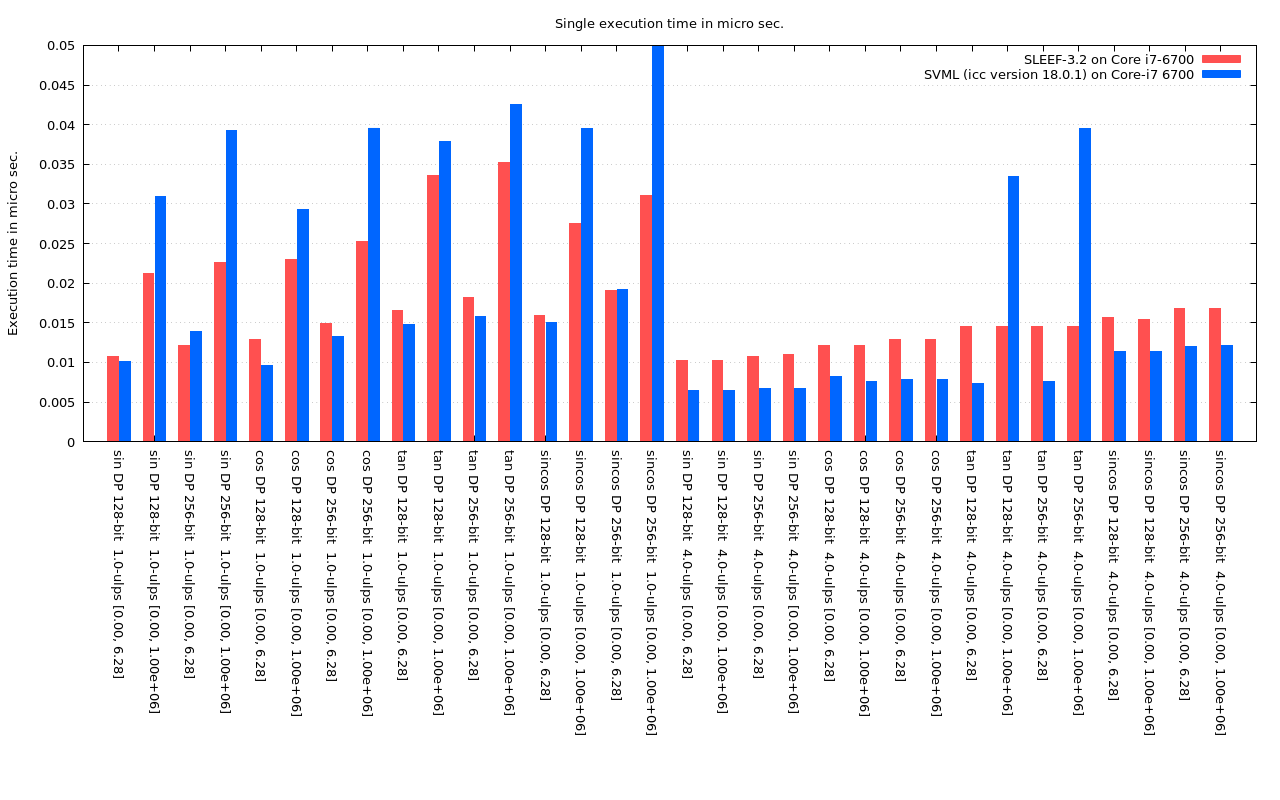
Fig. 6.1: Execution time of double precision trigonometric functions
The graphs below show comparison of the execution time between SLEEF-3.2 compiled with GCC-7.2 and Intel SVML included in Intel C Compiler 18.0.1.
The execution time of each function is measured by executing each function 10^8 times and taking the average time. Each time a function is executed, a uniformly distributed random number is set to each element of the argument vector(each element is set a different value.) The ranges of the random number for each function are shown below. Argument vectors are generated before the measurement, and the time to generate random argument vectors is not included in the execution time.
The accuracy of SVML functions can be chosen by compiler options, not the function names. "-fimf-max-error=1.0" option is specified to icc to obtain the 1-ulp-accuracy results, and "-fimf-max-error=5.0" option is used for the 5-ulp-accuracy results.
Those results are measured on a PC with Intel Core i7-6700 CPU @ 3.40GHz with Turbo Boost turned off. The CPU should be always running at 3.4GHz during the measurement.
Click graphs to magnify.

Fig. 6.1: Execution time of double precision trigonometric functions
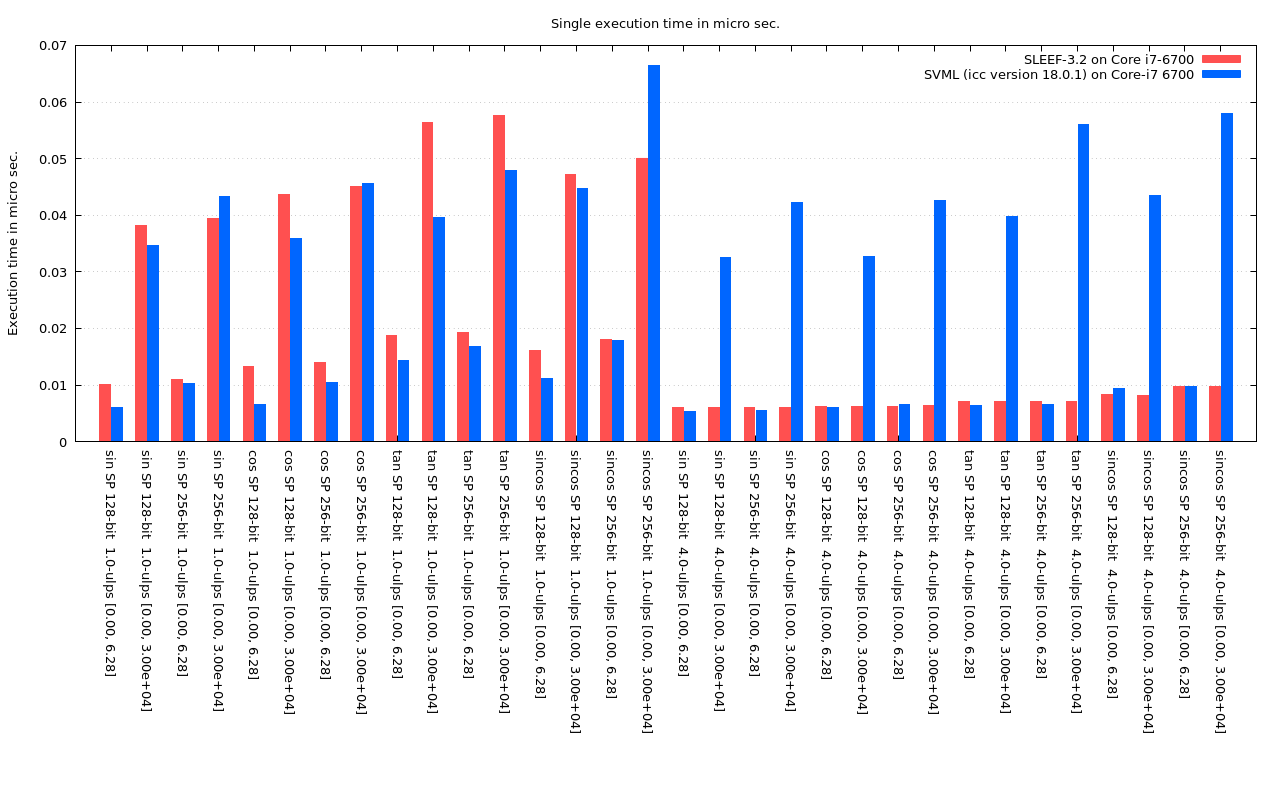
Fig. 6.2: Execution time of single precision trigonometric functions
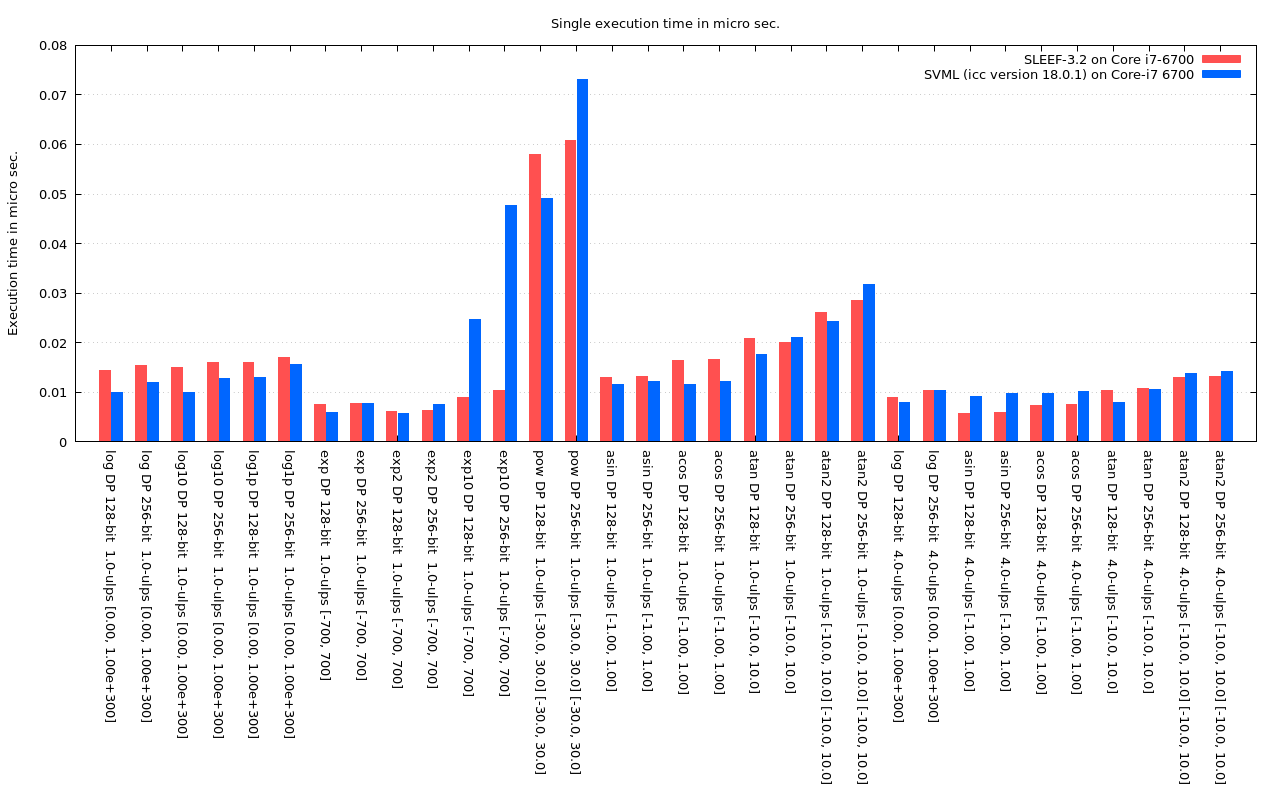
Fig. 6.3: Execution time of double precision log, exp, pow and inverse trigonometric functions
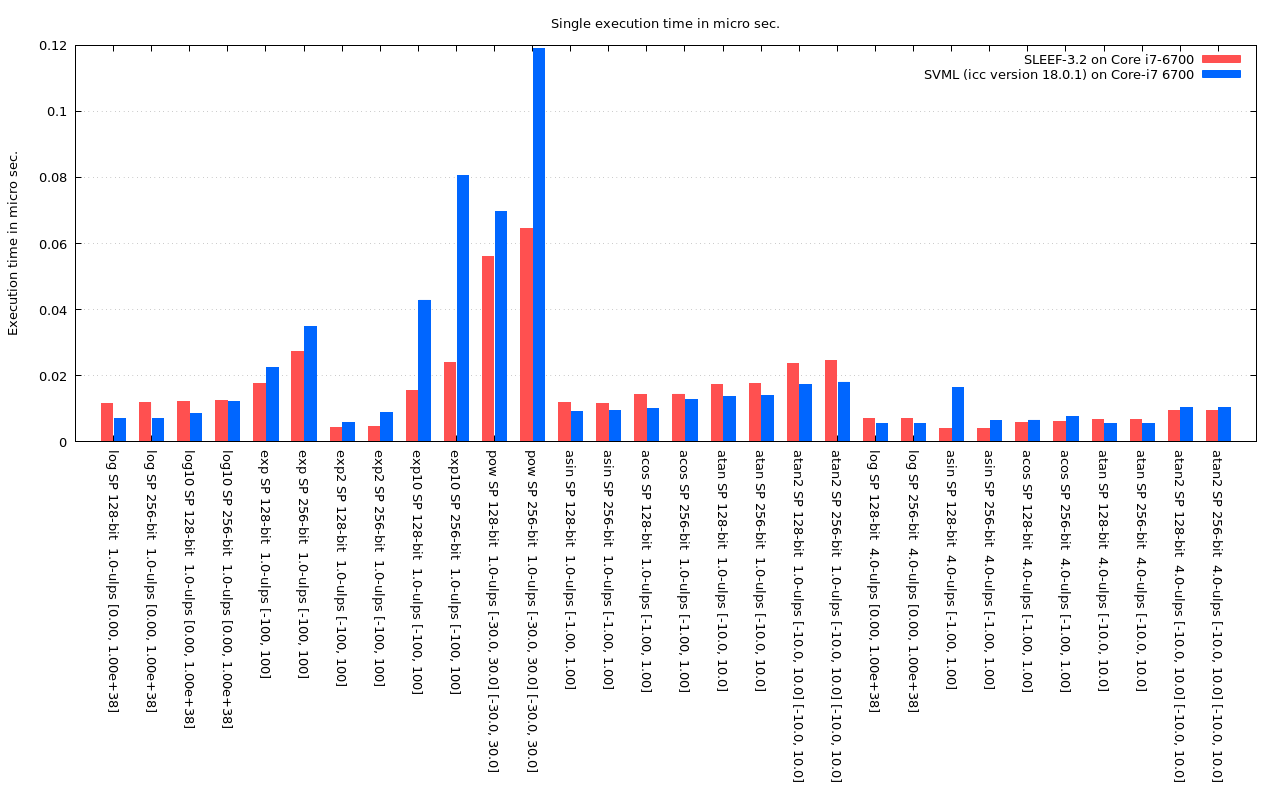
Fig. 6.4: Execution time of single precision log, exp, pow and inverse trigonometric functions
Below is the result of performance comparison between SleefDFT and FFTW3. The graphs show the performance of complex transform by both libraries, with the following settings.
The vertical axis represents the performance in Mflops calculated in the way indicated in the FFTW web site. The horizontal axis represents log2 of the size of transform. Execution plans were made with SLEEF_MODE_MEASURE mode and FFTW_MEASURE mode, respectively.

Fig. 6.5: Performance of transform in double precision on Ryzen 9 7950X

Fig. 6.6: Performance of transform in single precision on Ryzen 9 7950X
Below is the result of comparison on M1 MacBook Pro 16-inch with the following settings.

Fig. 6.7: Performance of transform in double precision on M1 MacBook Pro

Fig. 6.8: Performance of transform in single precision on M1 MacBook Pro
When benchmarking on your own, please keep in mind that the CPU clock must be fixed.